Pegadinhas em enunciados de provas do Enem tem algum valor didático?

Não irei fazer o Enem, mas irei participar de um processo seletivo que possui alguns exercícios de Análise Combinatória. Decidi fazer este artigo porque, atualmente escrever sobre um assunto é uma das formas que eu encontrei de estudar. Seria apenas um fichamento, um rascunho que eu nem iria publicar, porém uma pegadinha em um dos enunciados me motivou a complementar um pouco o texto, com uma opinião pessoal sobre didática no ensino da Matemática.

Neste excelente vídeo, recebi uma importante dica: A primeira coisa que é importante ao se analisar um problema de análise combinatória é a seguinte questão: a ordem importa?

1. Se sim, respondemos a nós mesmos (ahhã…). O que remete a: Arranjo!
2. Se não, vamos de Combinação. (Olha a rima Lombardi….)

Mas o que seria um arranjo?

Vamos pegar o exemplo citado no vídeo. Quantos conjuntos de 3 valores distintos que nós podemos formar com os números {1,2,3,4,5}?

Pensando em algo mais palpável para vida real, quantos pódios de Fórmula 1 diferentes podem acontecer com 5 pilotos competindo (José, João, Chico, Huguinho e Luizinho)?  Veja que neste exemplo, a ordem importa.

1. José em Primeiro, João em Segundo e Chico em Terceiro é um pódio.
2. Chico em Primeiro, João em Segundo e José em Terceiro é outro pódio.

Como a ordem dos elementos importa (ahã) o arranjo será utilizado. A fórmula literal  do arranjo consiste em “a quantidade  n de elementos, tomados pê a pê, resulta no fatorial de n dividido por n – p“. No nosso exemplo n é a quantidade de pilotos 5 e p são os valores distintos 3. A fórmula resulta em :

Substituindo os valores, temos:

60 maneiras de montar um pódio com 5 pilotos em posições diferentes.

Agora e a combinação? Vamos imaginar a situação onde eu quero montar pódios onde a ordem dos pilotos não importa, não entra no cálculo. Apenas quero agrupar os elementos. Neste caso:

1.  José em Primeiro, João em Segundo e Chico em Terceiro é um pódio.
2. Chico em Primeiro, João em Segundo e José em Terceiro é o mesmo pódio.

Se a ordem não importa (Não!) vamos de combinação. E a fórmula da combinação basicamente é a seguinte: “A combinação de n elementos tomados pê a pê resultado num fatorial de n dividido por p fatorial vezes (n – p) fatorial“. Resulta nesta fórmula abaixo.

Como no nosso problema o valor de n =5 e o valor de p =3, basta substituirmos para obtermos o valor de  10 combinações.

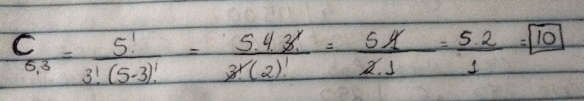
Através deste exercício, vi basicamente que o lance da análise combinatória é conseguir identificar no enunciado quem é p e quem é n e depois jogar para as fórmulas. Agora  vou tentar reproduzir fielmente a questão do Enem que é passada no vídeo, apontar os problemas que tive para resolver essa questão e fazer uma análise do que eu acho a respeito dela.

“Numa cartela com 60 números disponíveis, um apostador escolhe de 6 a 10 números. Dentre os números disponíveis, serão escolhidos apenas 6. O apostador será premiado caso os 6 números sorteados estejam entre os números escolhidos por ele numa mesma cartela.”

Cinco apostadores, cada um com R$ 500,00 para apostar, fizeram as seguintes opções:

• Arthur : 250 cartelas com 6 números escolhidos.
• Bruno: 41 cartelas com 7 números escolhidos e 4 cartelas com 6 números escolhidos.
• Caio: 12 cartelas com 8 números escolhidos e 10 cartelas com 6 números escolhidos.
• Douglas: 4 cartelas com 9 números escolhidos.
• Eduardo: 2 cartelas com 10 números escolhidos.

Responda: Os dois apostadores com maiores probabilidades de serem premiados são:

1. Caio e Eduardo
2. Arthur e Eduardo
3. Bruno e Caio
4. Arthur e Bruno
5. Douglas e Eduardo

Meu primeiro erro ao tentar resolver essa questão foi ao tentar achar o espaço amostral. Inicialmente imaginei n sendo 60 e os números disponíveis na cartela como sendo p. (antes do Ricieri eu tinha vergonha de assumir esses erros). Desta forma, para cada um dos apostadores eu teria uma combinação de 60 elementos tomados de p em p.

Ainda não consegui respostas para o motivo desta abordagem não ser válida, mas após verificar a resposta no vídeo, fiquei me questionando se o quantidade de números disponíveis na cartela seria algo realmente necessário ao problema e reescrevi na minha mente o seguinte enunciado abaixo. Ao invés de números, usei novamente pilotos de corrida. Não muda nada no conceito, mas pelo menos para mim, ficou bem mais fácil de entender o que aconteceu.

“Numa casa de apostas, é possível comprar diferentes bilhetes para tentar adivinhar os seis pilotos vencedores de uma corrida. Os bilhetes, lhe dão um leque de opções entre 6 a 10 pilotos. Cinco pessoas compraram as seguintes apostas“:

• Arthur comprou 250 cartelas com 6 opções de pilotos.
• Bruno comprou 41 cartelas com 7 opções de pilotos e 4 cartelas com 6 opções de pilotos.
• Caio comprou 12 cartelas com 8 opções de pilotos e 10 cartelas com 6 opções de pilotos.
• Douglas comprou 4 cartelas com 9 opções de pilotos.
• Eduardo comprou  2 cartelas com 10 opções de pilotos.

Baseando-se se nos bilhetes comprados, quais apostadores terão mais chances de adivinhar os 6 colocados?

Você consegue concordar comigo que são os mesmos enunciados? Se o total geral de pilotos e o valor das apostas com menos ou mais pilotos não vai interferir no resultado por qual motivo eu vou citar essa informação idiota?

Agora que já estamos com um enunciado um pouco mais simples, vamos tentar calcular cada uma das apostas.

•  Arthur : 250 cartelas com 6 números escolhidos
  • Se o cara comprou 250 cartelas, ele deseja que que sejam 6 números distintos. Porque senão ele vai pagar por duas cartelas, que fazem uma mesma aposta. (Ou seja, a ordem importa? Naaao – Combinação). Para resolver este problema teremos que usar combinações, mas pro caso do Arthur não será necessário o uso de fórmulas. Como cada aposta só terá 6 opções, os 250 cartões já virão praticamente marcados e o Arthur terá 250 chances de acertar os vencedores.
• Bruno: 41 cartelas com 7 números escolhidos e 4 cartelas com 6 números escolhidos
  • Chegamos enfim na Análise combinatória. Se em cada cartela há 7 pilotos e o apostador só pode escolher 6, temos n = 7 e p = 6. Colocando nas fórmulas de combinação acima temos o valor de 7 multiplicado por 41 cartelas, somado a 4 cartelas de 6 pilotos que estarão completamente preenchidas: 291 chances de acertar os pilotos vencedores.
• Caio: 12 cartelas com 8 números escolhidos e 10 cartelas com 6 números escolhidos 
  •  Aqui o mesmo caso n = 8 e p =6. Resultado 336 + 10 cartelas preenchidas = 346 chances disponíveis.
• Douglas: 4 cartelas com 9 números escolhidos
  • Aqui sendo n = 9 e p = 6  temos 84 opções em cada cartela. Sendo 4 cartelas temos 336 chances disponíveis
• Eduardo:  2 cartelas com 10 números escolhidos
  • Assumindo n =10  p = 6 chegamos no resultado de 210 chances para cada cartela. Sendo duas cartelas : 420 chances disponíveis.

Ou seja, Caio (346) e Eduardo (420) terão mais chances disponíveis de acertar.

 Valor didático das pegadinhas em Enunciados

Gostaria de fazer uma reflexão sobre o acontecido. Não sei quais os seus critérios para classificar alguém como inteligente, mas eu infelizmente não consigo aceitar que o critério de que colocar”pegadinhas” e “tumultuar” os desafios com informações inúteis possa ser um caminho para separar pessoas “inteligentes” de pessoas “não-inteligentes“. Neste problema de AC, a informação do preço das cartelas, quantidade de números disponíveis na cartela e o valor que cada sujeito tinha para apostar, poderiam ser descartadas tranquilamente. Isso foi colocado aí por pura sacanagem.

Eu acredito que esse tipo de coisa serve apenas para fazer as pessoas tomarem raiva da Matemática. E foi com uma grande alegria descobri que outras pessoas também acham a mesma coisa.

Pelo que percebi neste caso aqui, a diferença entre uma questão simples e uma questão bastante complexa foi apenas a quantidade de informação desnecessária no enunciado. Partindo do ponto que na escola estamos preparando as pessoas para um mercado de trabalho cada vez mais exigente, não seria melhor tentar formar pessoas sucintas? Que sejam precisas ao apresentar informações?

Não sou professor e talvez identificar pegadinhas e retirar informações desnecessárias de um enunciado, seja uma demonstração de habilidade em interpretação de texto e análise do aluno.E até considero que os caras que elaboram provas pro Enem e exercícios de livros do ensino médio,  façam essas pegadinhas com a melhor das intenções.

Mas olhando os nossos resultados de Matemática no ensino médio, fico pensando: será que isso realmente gera bons alunos? Será que isso realmente tá funcionando?